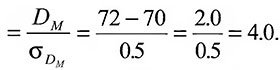Психологическая библиотека
ВВЕДЕНИЕ В ПСИХОЛОГИЮ.Учебник для студентов университетов
М., 1999.
Приложение.
Статистические методы и измерения
Приложение. Статистические методы и измерения
Значительная часть работы психолога состоит из проведения измерений — либо в лаборатории, либо в полевых условиях. Это могут быть измерения движений глаз младенца при первом воздействии нового стимула; регистрация кожно-гальванической реакции людей во время стресса; подсчет числа попыток, необходимых для обуславливания обезьяны с префронтальной лоботомией; определение показателей вступительных оценок среди учеников, использующих компьютеризованное обучение, или подсчет количества пациентов, у которых наступило улучшение после того или иного вида психотерапии. Во всех этих примерах операция измерения дает числа; задача психолога — интерпретировать их и прийти к некоторому общему выводу. Основной инструмент для этой задачи — статистика, дисциплина, имеющая дело со сбором числовых данных и проведением заключений на их основе. Цель данного приложения — рассмотреть некоторые статистические методы, играющие важную роль в психологии.
Это приложение написано в предположении, что проблемы, возникающие у студентов со статистикой, по сути есть проблемы ясного представления о полученных данных. Вводное знакомство со статистикой не выходит за рамки возможностей любого, кто достаточно разбирается в алгебре, чтобы использовать знаки «плюс» и «минус», а также подставлять числа вместо букв в уравнениях.
Описательная статистика
Статистика служит прежде всего для сокращенного описания больших объемов данных. Предположим, нам надо изучить показатели на вступительных экзаменах в колледж для 5000 учащихся, записанные на карточках в регистратуре. Эти показатели являются сырыми данными. Перелистывание карточек вручную даст нам некоторое впечатление о показателях учащихся, но удержать все это в голове будет невозможно. Поэтому мы делаем из этих данных своего рода резюме, усредняя все показатели или находя максимальную и минимальную величину. Эти статистические резюме облегчают запоминание и обдумывание данных. Такие резюмирующие высказывания называют описательной статистикой.
Частотное распределение
Элементы сырых данных становятся постижимы, когда они сгруппированы в частотное распределение. Чтобы сгруппировать данные, мы должны сначала поделить шкалу, по которой они измерялись, на интервалы, и затем посчитать, сколько элементов приходится на каждый интервал. Интервал, в котором группируются величины, называется групповым интервалом. Решение о том, на сколько групповых интервалов надо разбить данные, не определяется каким-либо правилом, а исходит от решения исследователя.
В табл. П1 показана выборка сырых данных, отражающих показатели 15 учащихся на вступительных экзаменах в колледж. Показатели приведены в том порядке, в каком учащиеся сдавали экзамен (у первого учащегося показатель был 84, у второго — 61 и т. д.). В табл. П2 эти же данные представлены в виде частотного распределения, для которого групповой интервал был установлен равным 10. На интервал от 50 до 59 приходится один показатель, на интервал от 60 до 69 — два и т. д. Заметьте, что большинство показателей приходятся на интервал от 70 до 79 и что ни один показатель не ниже интервала 50-59 или выше интервала 90-99.
Таблица П1. Сырые показатели
84 |
75 |
91 |
(Показатели 15 учащихся на вступительных экзаменах в колледж, приведенные в том порядке, в каком учащиеся сдавали экзамен.)
Таблица П2. Частотное распределение
Групповые интервалы |
Число лиц в группе |
50-59 |
1 |
60-69 |
3 |
70-79 |
7 |
80-89 |
3 |
90-99 |
1 |
Показатели из табл. П1, разбитые на групповые интервалы.
Частотное распределение легче понять, когда оно представлено графически. Наиболее широко применяемая графическая форма — это частотная гистограмма; ее пример показан в верхней части рис. П1. Гистограммы составляются путем рисования полос, основания которых задаются групповыми интервалами, а высота — соответствующими частотами групп. Еще один способ представления частотного распределения в графической форме — огибающая частоты, пример которой показан в нижней части рисунка П1. При построении огибающей частоты групп отмечаются напротив середины интервала групп, а затем эти точки соединяются прямыми линиями. Для завершения картины на каждом конце распределения добавляется еще один класс; поскольку у этих классов частота нулевая, оба конца получившейся фигуры окажутся на горизонтальной оси. Огибающая частоты дает ту же информацию, что и частотная гистограмма, но состоит из ряда соединенных отрезков, а не из полосок.
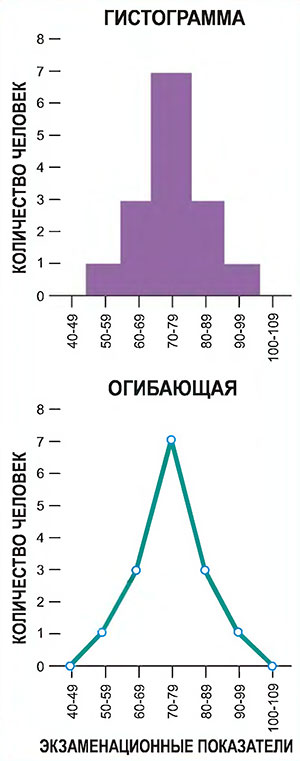
Здесь отображены данные из табл. П2. Вверху — частотная гистограмма, внизу — огибающая частоты.
На практике число элементов получается гораздо большим, чем то, что отражено на рис. П1, но на всех рисунках этого приложения показано минимальное количество данных, так чтобы вы могли легко проверить этапы размещения в таблице и на графике.
Меры среднего
Мера среднего — это просто показательная точка на шкале, сжато отражающая особенность имеющихся данных. Обычно используются три меры среднего: среднее значение, медиана и мода.
Среднее значение (или просто среднее) — это знакомое нам арифметическое среднее, получающееся при сложении всех величин и делении полученной суммы на их количество. Сумма сырых величин из табл. П1 равна 1125. Если поделить ее на 15 (общее количество величин), то среднее будет 75.
Медиана — отметка среднего элемента последовательности, полученной путем расположения всех величин по порядку и затем отсчета к середине, начиная с любого конца. Если 15 величин из табл. П1 расположить по порядку от самого большого к самому малому 8-я величина с любого конца будет равна 75. Если исходное количество величин будет четным, то мы просто считаем среднее от тех двух, которые оказываются в середине.
Мода — это самый часто встречающийся показатель в данной выборке. Самая частая величина в табл. П1 — это 75, следовательно, мода этого распределения равна 75.
При нормальном распределении, когда величины распределены поровну с каждой стороны от середины (как на рис. П1), среднее, медиана и мода одинаковы. Это не так для скошенных, или несимметричных, распределений. Предположим, нам надо проанализировать времена отправления утреннего поезда. Обычно поезд отправляется вовремя; случается, он отправляется позже, но он никогда не уходит раньше времени. У поезда с отправлением по расписанию в 08:00 время отправления в течение недели может оказаться таким:
Пн: 08:00 |
Cpeднee = 08:07 |
Это распределение времен отправления является скошенным из-за двух запоздавших отправлений; они увеличивают среднее время отправления, но не сильно влияют на медиану и моду.
Важно понять смысл скошенного распределения, поскольку иначе разницу между медианой и средним иногда трудно уловить (рис. П2). Если, например, руководство фирмы и ее профсоюз спорят из-за благосостояния работников, средняя величина расходов на зарплату и их медиана могут сдвинуться в противоположных направлениях. Предположим, фирма поднимает зарплату большинству сотрудников, но урезает зарплату высшим управленцам, которые были слишком высоко на шкале оплаты; тогда медиана зарплаты может подняться вверх, тогда как средняя величина зарплаты снизится. Сторона, стремящаяся показать, что зарплата возросла, выберет в качестве индикатора медиану, а сторона, стремящаяся показать снижение зарплаты, выберет среднее.
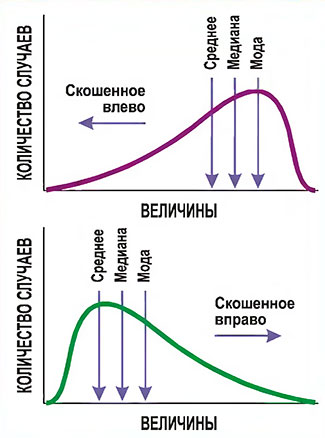
Заметьте, что скос распределения имеет то направление, в котором спадает его хвост. Заметьте также, что у скошенного распределения среднее, медиана и мода не совпадают; медиана обычно находится между модой и средним.
Меры вариации
Как правило, о распределении нужно знать больше, чем могут показать меры среднего. Нужна, например, мера, которая может сказать, расположен ли пучок величин близко к их среднему или широко разбросан. Мера разброса величин относительно среднего называется мерой вариации.
Показатель вариации полезен как минимум в двух отношениях. Во-первых, он показывает репрезентативность среднего. Если вариация невелика, то известно, что отдельные величины будут близки к среднему. Если вариация большая, то такое среднее нельзя с большой уверенностью использовать в качестве репрезентативной величины. Предположим, что шьется партия готовой одежды без снятия конкретных мерок. Для этого полезно знать средний размер этой группы людей, но также важно знать и разброс их размеров. Зная вариацию, можно сказать, насколько должны варьироваться изготовляемые размеры.
Для иллюстрации посмотрим на данные рис. П3, где приведены частотные распределения показателей вступительных экзаменов для двух классов из 30 учащихся. В обоих классах средний показатель один и тот же — 75, но они очевидно различаются по степени вариации. Показатели всех учащихся из класса А расположены близко к среднему, тогда как показатели учащихся из класса Б разбросаны в широком диапазоне. Нужны какие-то меры, чтобы точнее определить, чем различаются эти распределения. Психологи часто используют три меры вариации: размах, дисперсия и стандартное отклонение.
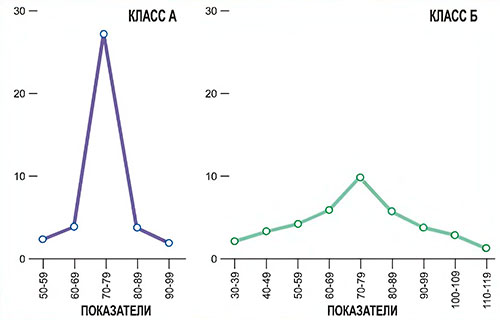
Как легко видеть, пучок показателей у класса А ближе к среднему, чем показатели класса Б, хотя само среднее в обоих классах идентично — 75. У класса А все показатели попадают между 60 и 89, причем большинство из них приходится на интервал от 70 до 79. У класса Б показатели распределены относительно равномерно по всему диапазону от 40 до 109. Это различие между двумя распределениями в разбросе можно оценить по показателю стандартного отклонения, которое у класса А меньше, чем у класса Б.
Чтобы упростить арифметические вычисления, предположим, что пять учащихся из каждого класса захотели поступить в колледж и что их суммарные оценки на вступительных экзаменах были такие:
Показатели учащихся из класса А:
73, 74, 75, 76, 77 (среднее = 75)
Показатели учащихся из класса Б:
60, 65, 75, 85, 90 (среднее = 75)
Теперь подсчитаем для этих двух выборок меры вариации.
Размах — это разброс между наивысшей и наинизшей величиной. Размах показателей у пяти учащихся из класса А равен 4 (от 73 до 77); размах показателей учащихся класса Б равен 30 (от 60 до 90).
Размах легче подсчитать, но дисперсия и стандартное отклонение используются чаще. Это более чувствительные меры вариации, поскольку они учитывают все величины, а не только крайние величины, как размах. Дисперсия показывает, насколько составляющие распределение величины отстоят от средней величины этого распределения. Чтобы вычислить дисперсию, сначала подсчитаем отклонения каждой величины (d) от среднего, вычтя из среднего каждую величину (табл. П3). Затем надо каждую разницу возвести в квадрат, чтобы не было отрицательных чисел. Наконец, эти отклонения складываются вместе и делятся на общее количество отклонений, давая в результате средний квадрат отклонения. Средний квадрат отклонения называется дисперсией. Проделав это с данными из рис. П3, мы обнаружим, что дисперсия у класса А равна 2,0, а у класса Б — 130. Очевидно, что у класса Б вариативность показателей значительно сильнее.
Таблица П3. Вычисление дисперсии и стандартного отклонения

Показатели выборок из двух классов представлены в виде, удобном для вычисления стандартного отклонения. На первом этапе вычитаем среднее из каждого показателя (среднее = 75 в обоих классах). В результате получаем положительные величины d для показателей, которые больше среднего, и отрицательные для тех, которые меньше его. Когда полученные величины будут возведены в квадрат, знак минус пропадет (следующая колонка в табл. П3). Возведенные в квадрат разности складываются и делятся на N — количество элементов выборки, в нашем случае N = 5. Извлекая квадратный корень, получаем стандартное отклонение. [В этом ознакомительном изложении мы везде будем использовать ? (сигма). Однако в научной литературе для обозначения стандартного отклонения выборки используется маленькая буква s, а через а обозначают стандартное отклонение для всей группы. Кроме того, при вычислении стандартного отклонения для выборки (s) сумма всех d2 делится не на N, а на N-1. В случае достаточно больших выборок, однако, использование N-1 вместо N мало влияет на величину стандартного отклонения. Для упрощения объяснений мы не будем различать здесь стандартное отклонение выборки и группы и используем для них одну и ту же формулу. Обсуждение этого момента см. в: Phillips (1992).]
Неудобство дисперсии состоит в том, что она выражена в единицах измерения, возведенных в квадрат. Поэтому величина дисперсии, равная 2 у класса А, не означает, что его усредненные показатели отличаются от среднего на 2 пункта. Она показывает, что 2 — это результат усреднения возведенных в квадрат значений, на которые показатели отличаются от среднего. Чтобы получить меру отклонения, выраженную в первоначальных единицах измерения (в данном случае это количество единиц, набранных на экзамене), надо просто извлечь из дисперсии квадратный корень. Результат называют стандартным отклонением. Оно обозначается греческой буквой σ (сигма), используемой также в некоторых других статистических вычислениях, которые мы обсудим вкратце. Стандартное отклонение вычисляется по следующей формуле:
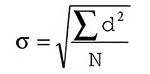
Статистические выводы
Теперь, познакомившись со статистикой как способом описания данных, мы готовы обратиться к интерпретации данных — тому, как из них делают выводы.
Группа и выборки
Прежде всего, необходимо различать группу и выборку из этой группы. Бюро переписи Соединенных Штатов пытается описать население в целом путем получения описательного материала по возрасту, семейному положению и т. д. обо всех жителях страны. Слово группа (population) годится для бюро переписи, поскольку оно представляет всех людей, живущих в США.
В статистике слово «группа» не ограничено людьми, животными или предметами. Группой могут быть все величины температур, зарегистрированные термометром в течение последнего десятилетия, все слова английского языка или любой другой определенный запас данных. Часто у нас нет доступа ко всей группе, и тогда мы пытаемся представить ее по выборке, взятой в случайном (непредвзятом) порядке. Можно задаться каким-либо вопросом о случайно отобранной части людей, как это сделало Бюро переписи в некоторых недавних переписях; можно вывести среднюю температуру, снимая показания термометра в определенное время и не ведя непрерывной записи; можно оценить количество слов в энциклопедии, подсчитав слова на случайно выбранных страницах. Во всех этих примерах делается выборка из группы. Если какие-либо из этих процессов повторить, результаты будут слегка различны вследствие того, что выборка не полностью отражает группу в целом и, следовательно, содержит ошибки выборки. Именно здесь вступают в игру статистические выводы.
Выборку данных из группы собирают, чтобы сделать вывод об этой группе. Можно изучить выборку данных переписи, чтобы узнать, стареет ли население, например, и существует ли тенденция миграции в пригородные зоны. Сходным образом, экспериментальные результаты изучаются, чтобы определить, какое воздействие экспериментальные манипуляции оказали на поведение — повлияла ли громкость на порог восприятия высоты звука, или оказывают ли особенности воспитания существенное влияние на последующую жизнь. Чтобы делать статистические выводы, надо оценить отношения, на которые указывают данные выборки. Такие выводы всегда имеют некоторую степень неопределенности из-за ошибок выборки. Если статистические испытания показывают, что величина эффекта, обнаруженная в данной выборке, достаточно велика (относительно оценки ошибки выборки), то можно быть уверенным, что наблюдаемый в данной выборке эффект существует и у группы в целом.
Таким образом, статистический вывод связан с необходимостью сделать вывод или суждение относительно некоторой характеристики группы, основываясь только на информации, полученной о выборке из этой группы. В качестве знакомства со статистическим выводом мы рассмотрим нормальное распределение и его применение при интерпретации стандартного отклонения.
Нормальное распределение

Устройство держат вверх ногами, пока все стальные шарики не скатятся в резервуар. Затем устройство переворачивают и держат вертикально, пока шарики, пройдя по полю со штырьками, не скатятся в 9 колонок-выемок внизу. Точное количество шариков, попавших в каждую колонку, в разных демонстрациях будет неодинаковым. Однако в среднем высота колонок из шариков будет примерно повторять нормальное распределение, когда самая высокая колонка будет в центре, а высоты остальных колонок будут снижаться в направлении к краям.
Когда большое количество данных собирают, представляют в табличном виде и отображают в виде гистограммы или огибающей, они часто образуют колоколообразное симметричное распределение, известное как нормальное распределение. Большинство его элементов располагаются вблизи среднего (верхняя точка колокола), и этот колокол резко спадает у самой большой и у самой малой величины. Такая форма кривой представляет особый интерес, поскольку она возникает и тогда, когда результат процесса основан на множестве случайных событий, все из которых происходят независимо. Демонстрационное устройство, показанное на рис. П4, позволяет увидеть, как из случайных событий складывается нормальное распределение. Случайный фактор — упадет ли стальной шарик влево или вправо каждый раз, когда он попадает в развилку, — приводит к симметричному распределению: больше шариков падают прямо посередине, но время от времени один из них достигает одного из крайних отделений. Это удобная визуализация того, что имеется в виду под случайным распределением, близким к нормальному распределению.
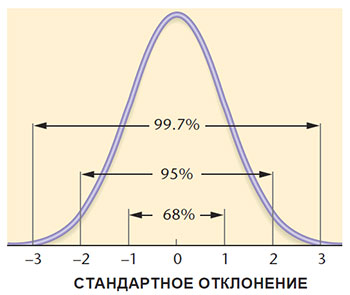
Кривую нормального распределения можно построить, используя стандартное отклонение и среднее. Площадью под кривой, лежащей левее -3σ и правее +3σ, можно пренебречь.
Нормальное распределение (рис. П5) — это математическое представление идеализованного распределения, приближенно создаваемого устройством, показанным на рис. П4. Нормальное распределение показывает вероятность того, что элементы в группе с нормальным распределением будут отличаться от среднего на любую заданную величину. В процентах на рис. П5 показана доля площади, лежащей под кривой между указанными величинами шкалы; общая площадь под кривой соответствует группе в целом. Примерно две трети всех случаев (68%) попадают в интервал между плюс и минус одним стандартным отклонением от среднего (±1σ); 95% всех случаев — в интервал ±2σ; и практически все случаи (99,7%) — в ±3σ.
Более подробный список площадей под частями кривой нормального распределения приведен в табл. П4.
Таблица П4. Площадь участков под кривой нормального распределения как часть общей площади под ней
Стандартное отклонение |
(1) Площадь левого участка от данного значения |
(2) Площадь правого участка от данного значения |
(3) Площадь участка между данным значением и средней |
-3,0 σ |
0,001 |
0,999 |
0,499 |
-2,5 σ |
0,006 |
0,994 |
0,497 |
-2,0 σ |
0,023 |
0,977 |
0,477 |
-1,5 σ |
0,067 |
0,933 |
0,433 |
-1,0 σ |
0,159 |
0,841 |
0,341 |
-0,5 σ |
0,309 |
0,691 |
0,191 |
0,0 σ |
0,500 |
0,500 |
0,000 |
+0,5 σ |
0,691 |
0,309 |
0,191 |
+1,0 σ |
0,841 |
0,159 |
0,341 |
+1,5 σ |
0,933 |
0,067 |
0,433 |
+2,0 σ |
0,977 |
0,023 |
0,477 |
+2,5 σ |
0,994 |
0,006 |
0,494 |
+3,0 σ |
0,999 |
0,001 |
0,499 |
Давайте при помощи табл. П4 проследим, как получаются величины 68% и 95%, показанные на рис. П5. В табл. П4 в третьей колонке находим, что между -1σ и средним лежит 0,341 общей площади и между +1σ и средним тоже 0,341 общей площади. В сумме эти величины дают 0,682, что на рис. П5 показано как 68%. Сходным образом площадь от -2σ до +2σ составит 2 х 0,477 = 0,954, показанные как 95%.
Шкалирование данных
Чтобы интерпретировать показатель, часто нужно знать, высокий он или низкий по отношению к другим показателям. Если человеку, сдающему водительский экзамен, требуется 0,500 сек, чтобы нажать на тормоз после сигнала опасности, как определить, быстро это или медленно? Считать ли, что студент сдал курс по физике, если его показатель на экзамене равен 60? Для ответа на такие вопросы надо вывести шкалу, с которой эти показатели можно сравнивать.
Ранжирование данных. Располагая показатели по рангу от высокого к низкому, мы получаем одну из таких шкал. Отдельный показатель интерпретируется по тому, на каком месте он располагается среди группы показателей. Например, курсанты военной академии Вест Пойнт знают, где они находятся в своем классе — возможно, 35-ми или 125-ми в классе из 400.
Стандартный показатель. Стандартное отклонение — удобная единица шкалирования, поскольку мы можем оценить, насколько далеко от среднего располагаются 1σ или 2σ (табл. П4). Величину произведения, в котором один сомножитель — стандартное отклонение, называют стандартным показателем. Многие шкалы, применяемые в психологических измерениях, основаны на принципе стандартного показателя.
Пример вычисления стандартного показателя. В табл. П1 приведены показатели, полученные 15 студентами на вступительных экзаменах. Не имея дополнительной информации, мы не знаем, являются ли эти показатели репрезентативными для группы всех поступавших. Однако предположим, что средний показатель на этих экзаменах был 75, а стандартное отклонение 10.
Каким же будет стандартный показатель у студента, набравшего на экзаменах 90 баллов? Насколько выше среднего лежит этот показатель, надо выразить в количестве стандартных отклонений:
Стандартный показатель для студента, с оценкой 90 равен:
(90-75)/10 = 15/10 = 1.5 σ.
В качестве второго примера возьмем учащегося с оценкой 53.
Стандартный показатель для оценки 53 равен:
(53 - 75)/10 = -22/10 = -2.2 σ
В этом случае показатель учащегося лежит ниже среднего на 2,2 стандартных отклонения. Таким образом, знак стандартного показателя (+ или -) говорит о том, выше или ниже среднего находится данный показатель, а его величина показывает, насколько далеко от среднего он расположен в единицах стандартных отклонений.
Насколько репрезентативно среднее?
Насколько хорошо среднее выборки отражает среднее всей группы? Если измерять рост у случайной выборки из 100 студентов колледжа, насколько хорошо среднее этой выборки предсказывает истинное среднее группы (то есть средний рост всех студентов колледжа)? Это все вопросы, связанные с выводом о группе на основе данных выборки.
Точность такого вывода зависит от ошибок выборки. Предположим, мы сделали две случайных выборки из одной и той же группы и для каждой из них подсчитали среднее. Какого различия между одним и другим средним можно ожидать в результате случая?
Последующие случайные выборки из той же группы будут давать разные средние, образуя распределение выборки средних вокруг истинного среднего данной группы. Эти выборки средних сами по себе являются величинами, для которых можно подсчитать стандартное отклонение. Это стандартное отклонение называется стандартной ошибкой среднего; оно обозначается σM и вычисляется по следующей формуле:
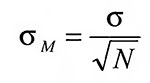
где σ — стандартное отклонение выборки, а N — количество случаев, по которым вычисляется каждое среднее.
Согласно этой формуле, величина стандартной ошибки среднего уменьшается с увеличением величины выборки; поэтому среднее, основанное на более крупной выборке, является более достоверным (оно скорее окажется ближе к истинному среднему всей группы). Этого можно было ожидать и на основе здравого смысла. Стандартная ошибка среднего ясно показывает, насколько неопределенно полученное среднее. Чем больше объем выборки, тем меньше неопределенность среднего.
Значимость различия
Во многих психологических экспериментах данные собираются по двум группам испытуемых; одна группа подвергается специфическим экспериментальным воздействиям, а другая служит контрольной. Вопрос в том, существует ли различие между средними показателями этих групп, и если есть, то выдерживается ли оно для всей группы, из которой были взяты эти две выборки. Проще говоря, отражает ли различие между двумя группами истинное различие или оно возникло вследствие ошибки выборки.
В качестве примера сравним показатели экзамена по чтению у выборки мальчиков-первоклассников с показателями у выборки девочек-первоклассниц. Что касается средних показателей, то они у мальчиков ниже, но здесь есть значительное перекрытие; некоторые мальчики справляются исключительно хорошо, а некоторые девочки — крайне плохо. Поэтому мы не можем принять это различие средних, не проведя тест на статистическую значимость. Только тогда можно будет решить, отражают ли наблюдаемые различия в выборке истинные различия в группе или же они объясняются ошибкой выборки. Если некоторые более одаренные девочки и некоторые более тупые мальчики оказались выбраны по чистой случайности, то различие можно объяснить ошибкой выборки.
В качестве еще одного примера предположим, что мы провели эксперимент по сравнению крепости рукопожатия у мужчин правшей и левшей. В верхней части табл. П5 показаны гипотетические данные такого эксперимента. Выборка из 5 мужчин-правшей в среднем на 8 кг сильнее выборки из 5 мужчин левшей. Что вообще можно вывести из таких данных о мужчинах левшах и правшах? Можно ли утверждать, что правши сильнее? Очевидно, нет, поскольку среднее, полученное у большинства правшей, не отличалось бы от среднего у большинства левшей; один примечательно отличающийся показатель величиной 100 говорит о том, что мы имеем дело с неопределенной ситуацией.
Таблица П5. Значимость различия
Пример 1
Сила сжатия в килограммах, |
Сила сжатия в килограммах, |
40 |
40 |
45 |
45 |
50 |
50 |
55 |
55 |
100 |
60 |
Сумма 290 |
Сумма 250 |
Среднее 58 |
Среднее 50 |
Пример 2
Сила сжатия в килограммах, |
Сила сжатия в килограммах, |
56 |
48 |
57 |
49 |
58 |
50 |
59 |
51 |
60 |
52 |
Сумма 290 |
Сумма 250 |
Среднее 58 |
Среднее 50 |
Два примера, показывающих различие между средними. Разница средних одинакова (8 кг) в верхней и нижней части таблицы. Однако, данные нижней части указывают на более надежное различие средних, чем данные в верхней части таблицы.
Теперь предположим, что в результате эксперимента получены результаты, показанные в нижней части той же табл. П5. Мы снова видим то же самое различие средних, равное 8 кг, но теперь эти данные вызывают большее доверие, поскольку показатели у левшей получились систематически ниже, чем у правшей. Статистика позволяет очень точно учесть надежность различий среднего, так чтобы при определении, какое из двух различий более надежно, не зависеть только от интуиции.
Эти примеры показывают, что значимость полученного различия зависит и от его величины, и от варьируемости сравниваемых средних. Зная стандартную ошибку среднего, можно вычислить стандартную ошибку различия между двумя средними σDM. Затем можно оценить полученное различие при помощи критического отношения — отношения полученной разницы средних (DM) к стандартной ошибке различия между средними:
Критическое отношение = |
|
Это отношение позволяет оценить значимость различия между двумя средними. Как простейшее правило, критическое отношение должно быть не менее 2,0, чтобы разница средних считалась значимой. Во всей этой книге выражение о «статистической значимости» разницы средних означает, что критическое отношение у них не меньше такого.
Почему в качестве статистически значимого выбрано критическое отношение, равное 2.0? Просто потому, что такая или большая величина может выпасть случайно только в 5% случаев. Откуда взялись эти 5%? Критическое отношение можно считать стандартным показателем, поскольку это просто разница двух средних, выраженная в числе стандартных ошибок. Обращаясь ко 2-й колонке табл. П4, замечаем, что вероятность того, что стандартное отклонение составляет 2,0 при случайном совпадении, равна 0,023. Поскольку вероятность отклонения в противоположную сторону тоже равна 0,023, общая вероятность составит 0,046. Это означает что когда средние групп одинаковы, критическое отношение может случайно оказаться равным 2,0 (или более) в 46 случаях из 1000, или в 5% случаев.
Элементарное правило, говорящее, что критическое отношение должно быть не менее 2,0, именно таково — это произвольное, но удобное правило, задающее 5%-ный уровень значимости. Следуя этому правилу, вероятность ошибочного решения о том, что разница средних существует, тогда как на самом деле это не так, будет меньше 5%. Не обязательно пользоваться 5%-ным уровнем; в некоторых экспериментах может потребоваться более высокая значимость, в зависимости от того, насколько допустима ошибка заключения.
Пример вычисления критического отношения. Для вычисление критического отношения надо определить стандартную ошибку разницы двух средних по следующей формуле:
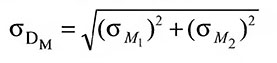
В этой формуле σМ1 и σМ2 — стандартные ошибки двух сравниваемых средних.
В качестве иллюстрации предположим, что нам надо сравнить достижения первоклассников — мальчиков и девочек на экзамене по чтению в США. Берется случайная выборка мальчиков и девочек и подвергается тестированию. Предположим, что средний показатель у мальчиков равен 70 при стандартной ошибке среднего 0,40, а средний показатель у девочек — 72 при стандартной ошибке среднего 0,30. На основе этих выборок надо решить, есть ли это реальное различие между успехами мальчиков и девочек в чтении в группе в целом, Данные выборки показывают, что оценки у девочек больше, чем у мальчиков, но можно ли заключить, что мы получили бы то же самое, протестировав всех первоклассников США? Решить это позволяет критическое отношение.
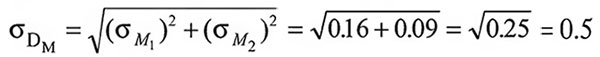
Критическое отношение |
|
Поскольку критическое отношение значительно выше 2,0, можно утверждать, что наблюдаемое среднее различие статистически значимо на 5%-ном уровне. Поэтому можно заключить, что между мальчиками и девочками существует надежное различие в успехах по чтению. Заметьте, что критическое отношение может быть положительным и отрицательным, в зависимости от того, какое среднее из какого вычитается; при интерпретации критического отношения учитывается только его величина, но не знак.
Коэффициент корреляции
Корреляцией называют параллельную вариацию двух величин. Предположим, что разрабатывается тест для предсказания успеваемости в колледже. Если это хороший тест, высокие показатели в нем должны связываться с высокой успеваемостью в колледже, а низкие — с низкой успеваемостью. Коэффициент корреляции позволяет точнее установить степень этой связи.
Корреляция как произведение моментов
Чаще всего коэффициент корреляции определяется методом произведения моментов; получаемый в результате индекс обычно обозначается маленькой буквой r. Вычисленный через произведение моментов коэффициент r варьируется между полной положительной корреляцией (r = +1,00) и полной отрицательной корреляцией (r = -1,00). Отсутствие всякой связи дает r = 0,00.
Корреляция вычисляется через произведение моментов по формуле:
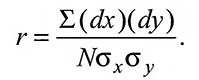
Здесь одну из парных мер называют x-показателем, а другую y-показателем, dx и dy — это отклонения каждого показателя от среднего; N — количество парных величин, а σx и σy — стандартные отклонения x-показателей и y-показателей.
Для определения коэффициента корреляции надо определить сумму произведений (dx) x (dy). Эту сумму вместе с вычисленными стандартными отклонениями для х-показателей и y-показателей можно затем подставить в формулу.
Пример вычисления корреляции через произведение моментов. Предположим, мы собрали данные, показанные в табл. П6. Для каждого испытуемого получено два показателя; первый — оценка на вступительных экзаменах (ее мы произвольно назовем x-показателем), а второй — оценки за первый курс (y-показатель).
Таблица П6. Вычисление корреляции через произведение моментов

На рис. П6 показан точечный график этих данных. Каждая точка отражает x-показатель и y-показатель данного человека; например, верхняя точка справа означает Андрея. Глядя на эти данные, легко обнаружить, что между х- и у-показателями существует некоторая положительная корреляция. Андрей получил наивысшую оценку на вступительном экзамене и также получил наивысшую отметку за 1-й курс; Дмитрий получил и там, и там самую низкую отметку. В показателях других студентов есть немного нерегулярности, так что мы знаем, что корреляция не полная; следовательно, r меньше 1,00.
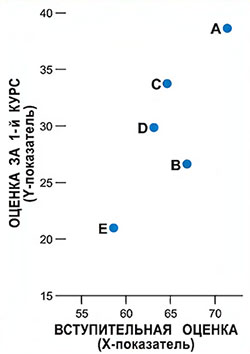
Мы подсчитаем корреляцию, чтобы проиллюстрировать этот метод, хотя на практике ни один исследователь не станет считать корреляцию для столь малого количества показателей. Подробности приведены в табл. П6. Согласно процедуре, приведенной в табл. П3, мы вычисляем стандартное отклонение x-показателей, а затем стандартное отклонение y-показателей. Затем мы вычисляем произведение (dx) x (dy) для каждого человека и для 5 случаев в общем. Подставляя полученные числа в уравнение, получаем r = +0.85.
Интерпретация коэффициента корреляции
Корреляцию можно использовать для прогнозирования. Например, если из опыта известно, что определенный вступительный тест коррелирует с отметками первокурсников, можно предсказать отметки на экзаменах за первый курс у тех начинающих студентов, которые этот тест проходили. Если корреляция полная, их отметки можно предсказать безошибочно. Но, как правило, r меньше 1,00 и в прогнозе есть определенные ошибки; чем ближе r к 0, тем больше ошибка прогноза.
Мы не сможем рассмотреть технические проблемы прогнозирования оценок первокурсников, исходя из оценок на вступительном экзамене или других аналогичных прогнозов, но можно рассмотреть смысл разной величины коэффициента корреляции. Очевидно, что если корреляция между х и у равна 0, то знание х не поможет предсказать у. Если вес человека не связан с интеллектом, то знание о весе ничего не дает для предсказания интеллекта. Другое полярное значение — полная корреляция — означало бы 100%-ную эффективность прогноза: зная х, можно было бы абсолютно точно предсказать у. Но что значат промежуточные величины r? Некоторое представление о значении промежуточной величины коэффициента корреляции можно получить из точечных диаграмм на рис. П7.
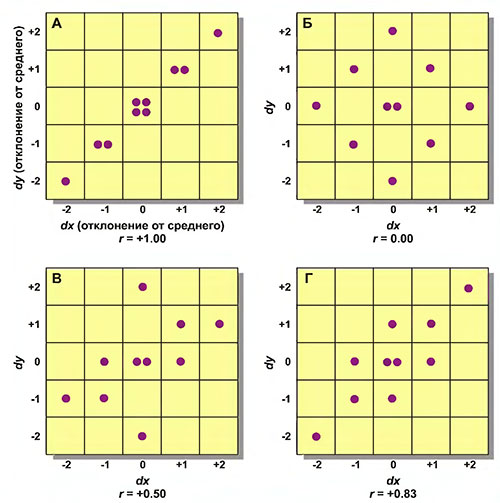
Каждая точка изображает оценки одного человека в двух экзаменах, х и у. На графике А все случаи падают на диагональ, и корреляция является полной (r = +1,00); если известна оценка человека по х, значит она будет такой же и по у. На графике Б корреляция равна 0; зная оценку человека по х, мы не сможем сказать, будет ли она у него такой же, выше или ниже по у. Например, из четырех человек со одинаковой средней оценкой, равной х (dx = 0), один получает очень высокую отметку по у (dy = +2), один — очень низкую (dy = -2), а два получают среднюю. На графиках В и Г существует диагональная тенденция отметок, так что высокая отметка по х имеет связь с высокой отметкой по у, а низкая отметка по х имеет связь с низкой отметкой по у, но связь эта неполная. Если на осях не будет обычных шкал, это никак не повлияет на интерпретацию. Например, если бы мы координатам х и у присвоили величины от 5 до 10 и затем подсчитали бы r для этих новых величин, коэффициент корреляции получился бы тем же самым.
В предыдущем обсуждении мы не обращали особого внимания на знак коэффициента корреляции, поскольку он не говорит о силе связи. Единственное различие между коэффициентами корреляции +0,70 и -0,70 — это то, что в первом случае увеличение х сопровождается увеличением у: а во втором увеличение х сопровождается уменьшением у.
Коэффициент корреляции — один из наиболее часто применяемых статистических инструментов в психологии, но одновременно это одна из тех процедур, которые чаще всего неверно используются. Те, кто им пользуется, часто упускают из виду, что r не указывает на причинно-следственную связь между х и у. Когда два набора показателей коррелируют, можно предположить, что у них есть некоторый общий причинный фактор, но нельзя считать, что один из них просто вызывает другой.
Корреляция иногда выглядит парадоксально. Например, было обнаружено, что корреляция между временем, затрачиваемым на учебу, и оценками в колледже имеет слегка отрицательную величину (-0,10). Если использовать причинную интерпретацию, то пришлось бы заключить, что лучший способ улучшить отметки — перестать учиться. На самом же деле отрицательная корреляция возникает здесь просто потому, что у некоторых студентов есть преимущество над остальными в получении высоких отметок (возможно потому, что они лучше были подготовлены к колледжу), так что те, кто затрачивает больше времени на учебу, — это часто те, кому высокие отметки даются труднее остальных.
Этот пример служит достаточным предупреждением против причинного понимания коэффициента корреляции. Случается, однако, что две переменных коррелируют и одна из них действительно является причиной другой. Поиск причины — дело логики, и корреляция может направлять экспериментаторов при проверке причинно-следственных отношений.