Психологическая библиотека
ВВЕДЕНИЕ В ПСИХОЛОГИЮ.Учебник для студентов университетов
М., 1999.
Часть IV. Научение, запоминание и мышление
Глава 9. Мышление и речь
Рассуждение
Когда мы мыслим суждениями, последовательность мыслей организованна. Иногда организация наших мыслей определяется структурой долговременной памяти. Мысль позвонить отцу, например, ведет к воспоминанию о недавнем разговоре с ним у вас дома, что, в свою очередь, ведет к мысли починить в вашем доме чердак. Но ассоциации в памяти — это не единственное средство организации мышления. Представляет интерес также организация, характерная для тех случаев, когда мы стараемся рассуждать. Здесь последовательность мыслей часто принимает форму обоснования, в котором одно высказывание представляет собой утверждение, или вывод, который мы хотим сделать. Остальные высказывания являются основаниями этого утверждения, или посылками этого вывода.
Дедуктивное мышление
Логические правила. В логике наиболее строгие доказательства имеют дедуктивную достоверность; это означает, что вывод доказательства не может быть ложным, если истинны все его посылки (Skyrms, 1986). Вот пример такого доказательства:
а. Если идет дождь, я возьму зонтик.
б. Идет дождь.
в. Следовательно, я возьму зонтик.
Насколько рассуждения обычных людей соответствуют рассуждениям логика? Когда нас спрашивают, является ли доказательство дедуктивно достоверным или нет, мы весьма точно оцениваем простые доказательства. Как мы выносим такого рода суждения? В некоторых теориях дедуктивного мышления полагается, что люди действуют подобно интуитивным логикам и применяют логические правила, пытаясь обосновать, что вывод доказательства следует из данных посылок. Для иллюстрации рассмотрим следующее правило:
«Если есть высказывание вида «Если р, то q» и еще одно высказывание р, то можно вывести высказывание q.»
По-видимому, взрослые знают это правило (возможно, бессознательно) и используют его для принятия решения о том, что приведенное доказательство достоверно. В частности, они идентифицируют первую посылку («Если идет дождь, я возьму зонтик») с частью «Если p, то q» этого правила. Вторую посылку («Идет дождь») они идентифицируют с частью р этого правила, и затем они выводят часть q («Я возьму зонтик»).
Следование правилам становится более осознанным, если усложнить доказательство. Приведенное правило мы применяем дважды, когда оцениваем следующее доказательство:
а. Если идет дождь, я возьму зонтик.
б. Если я возьму зонтик, я его потеряю.
в. Идет дождь.
г. Следовательно, я потеряю свой зонтик.
Применяя знакомое нам правило к высказываниям а и в, можно сделать вывод, что «я возьму зонтик»; а применяя это правило еще раз к высказыванию б и к выведенному высказыванию, можно заключить, что «я потеряю свой зонтик». Одним из лучших подтверждений тому, что люди используют подобные правила, является то, что количество правил, требуемых для доказательства, определяет трудность последнего. Чем больше требуется правил, тем более вероятно, что человек сделает ошибку, и тем больше времени у него уйдет на то, чтобы принять правильное решение (Rips, 1983, 1984).
Влияние содержания. Логические правила не охватывают всех аспектов дедуктивного мышления. Эти правила определяются только логической формой высказываний, наша же способность оценивать дедуктивное доказательство часто зависит также от содержания высказываний. Этот момент иллюстрируется в следующем эксперименте. Испытуемым предъявляют 4 карточки. В одном варианте каждая карточка имеет на одной стороне букву, а на другой — цифру (верхний ряд на рис. 9.7). Испытуемый должен решить, какие карточки следует перевернуть, чтобы определить правильность утверждения «Если на одной стороне карты гласная, то на другой ее стороне — четное число». Притом что большинство испытуемых правильно выбирали карточку с буквой «Е», менее 10% из них выбирали также карточку с цифрой «7», что является вторым правильным решением (чтобы убедиться в том, что карточка «7» — тоже правильное решение, заметьте, что если на другой ее стороне гласная, утверждение опровергается).
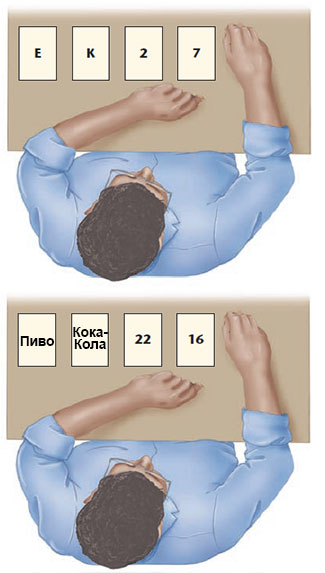
В верхнем ряду показан вариант задачи, в котором испытуемым надо было решить, какие две карточки следует перевернуть, чтобы проверить гипотезу «Если на одной стороне карточки гласная, то на другой — четное число». В нижнем ряду показан вариант задачи, в котором испытуемые решали, какие карточки следует перевернуть, чтобы проверить гипотезу «Если человек пьет пиво, ему должно быть больше 19» (из: Criggs & Сох, 1982; Wason & Johnson-Laird, 1972).
Значительно лучше, однако, испытуемые справлялись с другим вариантом этой задачи (нижний ряд рис. 9.7). В нем испытуемым надо было оценить утверждение «Если человек пьет пиво, ему должно быть больше 19». У каждой карточки на одной стороне было число, означающее возраст человека, а на другой — название напитка. С точки зрения логики этот вариант задачи идентичен первому (в частности, «Пиву» соответствует «Е», а «16» соответствует «7»); но теперь большинство испытуемых находили оба верных ответа (переворачивали карточки «Пиво» и «16»). Таким образом, содержание высказываний влияет на наше рассуждение.
Подобные результаты означают, что, встречаясь с дедуктивными задачами, мы не всегда пользуемся логическими правилами. Иногда мы применяем прагматические правила, менее абстрактные и более отвечающие повседневным задачам. Примером является правило разрешения, которое говорит: «Если надо предпринять определенное действие, то должно быть выполнено предварительное условие». Это правило знают большинство людей, и они применяют его, встречаясь с задачей о пиве, показанной внизу на рис. 9.7; то есть они обдумывают эту задачу с точки зрения разрешающего условия. Будучи активированным, это правило будет подталкивать их к поиску случаев невыполнения соответствующего предусловия (достижения 19 лет), что, в свою очередь, приведет их к выбору карточки «16». Напротив, в задаче с буквами и числами (верхняя часть рис. 9.7) правило разрешения не действует, поэтому нет причин для выбора карточки «7». Таким образом, от содержания задачи зависит, будет или нет активироваться прагматическое правило, что, в свою очередь, влияет на правильность рассуждения (Cheng, Holyoak, Nisbett & Oliver, 1986).
Решая задачу о пиве, испытуемые могут не только пользоваться правилами, но и воссоздавать в уме конкретную репрезентацию, или мысленную модель ситуации. Можно, например, представить себе двух человек, каждого с номером на спине и с напитком в руке. Затем можно исследовать эту мысленную модель и смотреть, что происходит, например, если у пьющего с числом 16 на спине в руке оказывается пиво. Согласно такому взгляду человек рассуждает при помощи мысленных моделей, предлагаемых содержанием задачи (Johnson-Laird, 1989).
Две только что описанные процедуры — применение прагматических правил и построение мысленных моделей — имеют нечто общее: они определяются содержанием задачи. Это отличает их от применения логических правил, на которые содержание задачи не должно влиять. Следовательно, чувствительность к содержанию задачи часто удерживает нас от действий, подчиняющихся интуитивной логике.
Индуктивное мышление
Логические правила. Логики отмечают, что доказательство может быть хорошим, даже если оно не имеет дедуктивной достоверности. Такого рода доказательства обладают силой индукции, что означает невероятность ложности заключения, если все посылки истинны (Skyrms, 1986). Вот пример строго индуктивного доказательства:
а. В колледже Митч специализировался на бухгалтерском учете.
б. Сейчас Митч работает в бухгалтерской фирме.
в. Следовательно, Митч — бухгалтер.
Это доказательство не является дедуктивно достоверным (возможно, Митчу надоели бухгалтерские курсы и он перешел на работу ночным сторожем в том единственном месте, где у него были связи). Индуктивная строгость, таким образом, — это вопрос вероятности, а не определенности; и (как считают логики) индуктивная логика должна основываться на теории вероятности.
Мы постоянно совершаем и оцениваем индуктивные доказательства. Полагаемся ли мы при этом на законы теории вероятности, как это делают логики и математики? Одним из относящихся сюда законов теории вероятности является правило объема базиса, утверждающее, что вероятность принадлежности чего-либо к определенному классу (например, принадлежности Митча к классу бухгалтеров) тем больше, чем больше существует членов этого класса (т. е. чем выше объем базиса этого класса). Так, вышеприведенное доказательство того, что Митч — бухгалтер, можно усилить, добавив к нему посылку, что Митч стал членом клуба, 90% членов которого — бухгалтеры.
Другой относящийся к нашему случаю вероятностный закон — это правило конъюнкции: вероятность высказывания не может быть меньше, чем вероятность этого же высказывания, сочетаемого с другим высказыванием. Например, вероятность того, что «Митч — бухгалтер», не может быть меньше, чем вероятность того, что «Митч — бухгалтер и зарабатывает более 40 000 долларов в год». Правило объема базиса и правило конъюнкции — это рациональные принципы индуктивного мышления; они подкреплены логикой, и большинство людей полагаются на них, когда эти правила выражены в явной форме. Однако в суматохе обыденного мышления люди часто нарушают эти правила, в чем мы скоро убедимся.
Эвристики. Эвристика — это упрощенная процедура, которую достаточно легко применять и которая часто позволяет получить правильный результат, однако результат, полученный таким образом, не обязательно будет правильным. Люди часто используют эвристики в повседневной жизни, поскольку находят их полезными. Однако, как следует из дальнейшего изложения, на эвристики далеко не всегда можно полагаться.
В ряде простых экспериментов ученые показали (Tversky & Kahneman, 1983, 1973), что, делая индуктивные суждения, люди нарушают некоторые основные правила теории вероятности. Особенно часты нарушения правила объема базиса. В одном эксперименте группе испытуемых сказали, что психологический совет провел интервью с 30 инженерами и 70 юристами (всего 100 человек) и составил описания их личностей. Испытуемым раздали несколько описаний и просили указать для каждого из них вероятность того, что данный человек является инженером. Некоторые описания были прототипами инженера (например: «Джека не интересует политика, свое свободное время он проводит в мастерской»); другие были нейтральными (например: «Дик — очень способный человек, и ему обещан настоящий успех»). Неудивительно, что эти испытуемые с большей вероятностью относили к инженеру прототипное описание, а не нейтральное. Другой группе испытуемых дали аналогичные инструкции и описания, и кроме того им сказали, что из этих 100 человек 70 были инженерами, а 30 — юристами (обратная пропорция относительно первой группы). Следовательно, объем базиса инженеров в этих группах был существенно разным. Но это различие фактически не дало никакого эффекта: испытуемые второй группы давали в основном те же оценки, что и испытуемые первой группы. Например, в обеих группах испытуемые с вероятностью 50 на 50 относили нейтральные описания к инженерам (тогда как с их стороны было бы рациональным с большей вероятностью относить нейтральные описания к профессии с более высоким объемом базиса). Испытуемые полностью игнорировали информацию о базисных объемах (Tversky & Kahneman, 1973).
Ничуть не большее внимание обращают люди и на правило конъюнкции. В одном исследовании испытуемым предъявляли следующее описание:
«Линда, 31 год, не замужем, откровенная и очень смышленая. В колледже специализировалась по философии... и серьезно интересовалась вопросами дискриминации».
Затем испытуемые оценивали вероятность следующих утверждений:
1. Линда — кассир в банке.
2. Линда — кассир в банке и активистка феминистского движения.
Предложение 5 является конъюнкцией предложения 4 с высказыванием «Линда — активистка феминистского движения». Явно нарушая правило конъюнкции, большинство испытуемых оценивали вероятность 5 выше, чем вероятность 4. Заметьте, что это — прямое заблуждение, поскольку всякая феминистка — банковский кассир является банковским кассиром, но некоторые банковские кассиры не являются феминистками, и Линда могла быть среди последних (Tversky & Kahneman, 1983).
Испытуемые в этом исследовании основывали свои суждения на том, что Линда больше похожа на банковского кассира и феминистку, чем просто на банковского кассира. Хотя испытуемых просили оценить вероятность, они вместо этого оценивали сходство Линды с прототипами понятий «банковский кассир» и «феминистка — банковский кассир». Таким образом, оценка сходства выполняет роль эвристики для оценки вероятности, где эвристика — это сокращенная процедура, которую относительно легко использовать и которая может приносить правильный ответ часто, хотя и не всегда. То есть люди используют эвристику сходства, потому что сходство часто связано с вероятностью и к тому же его легче вычислить. Применение эвристики сходства объясняет также, почему люди игнорируют объем базиса. В эксперименте с «инженером» и «юристом» испытуемые, видимо, рассматривали только сходство предъявленного описания со своими прототипами «инженера» и «юриста». Поэтому когда описание одинаково хорошо подходило и к «инженеру» и к «юристу», испытуемые считали того и другого равновероятными. Использование эвристики сходства может приводить к ошибкам даже экспертов.
Принцип сходства проявляется в еще одном распространенном случае рассуждения, когда, зная, что некоторые члены категории обладают определенным свойством, надо решить, есть ли это свойство у членов другой категории. В одном исследовании испытуемым надо было решить, какое из двух нижеследующих доказательств сильнее:
а. У всех малиновок есть сезамовидные кости.
б. Следовательно, у всех воробьев есть сезамовидные кости.
или
а. У всех малиновок есть сезамовидные кости.
б. Следовательно, у всех страусов есть сезамовидные кости.
Неудивительно, что испытуемые сочли первое доказательство сильнее, видимо потому, что малиновки более похожи на воробьев, чем на страусов. Такая опора на сходство кажется рациональной тем более, что она согласуется с представлением, что если предметы имеют много общих известных свойств, то у них, вполне вероятно, есть и общие неизвестные свойства. Однако видимость рациональности блекнет, когда мы переходим к оценкам испытуемыми другой пары доказательств:
а. У всех малиновок есть сезамовидные кости.
б. Следовательно, у всех страусов есть сезамовидные кости.
или
а. У всех малиновок есть сезамовидные кости.
б. Следовательно, у всех птиц есть сезамовидные кости.
Испытуемые сочли второе доказательство более сильным, видимо потому, что малиновки более сходны с прототипом птицы, чем с прототипом страуса. Но такое суждение ошибочно: если исходить из той же посылки (что у малиновок сезамовидные кости), наличие некоторого свойства у всех птиц не может быть более вероятным, чем наличие его у всех страусов, поскольку страусы на самом деле птицы. Опять мы видим, что интуиция, основанная на сходстве, может иногда приводить к заблуждению (Osherson et al., 1990).
Сходство — не единственный вид сильной эвристики; помимо нее существует также причинная эвристика. Люди оценивают вероятность ситуации по силе причинной связи между событиями в этой ситуации. Например, предложение 2 им кажется более вероятным, чем предложение 1:
1. В 2000 году в Калифорнии будет сильное наводнение, во время которого утонут более 1000 человек.
2. В 2000 году в Калифорнии будет землетрясение, которое вызовет сильное наводнение, во время которого утонут более 1000 человек.
Посчитать, что 2 вероятнее 1, — это еще одно нарушение правила конъюнкции (и, следовательно, еще одно заблуждение). В этот раз нарушение происходит потому, что в предложении 2 наводнение имеет сильную причинную связь с другим событием — землетрясением; тогда как в предложении 1 упоминается только наводнение и у него соответственно нет причинных связей.
Итак, использование эвристик часто приводит нас к игнорированию некоторых основных правил рассуждения, включая правило базисного объема и правило конъюнкции. Но не стоит быть слишком пессимистичным в отношении нашего уровня рациональности. Во-первых, эвристика сходства и причинности приводит в большинстве случаев к верным решениям. Во-вторых, при соответствующих обстоятельствах мы способны оценить уместность определенных логических правил для решения тех или иных задач и соответственно их применять (Nisbett et al., 1983). Так, читая этот материал и думая о нем, вы, возможно, сумели убедиться в том, что правило базисного объема и правило конъюнкции играют важную роль в решении задач.




